3. Papiroflexia y Matemáticas

Fuente: Wikpedia.

Ya desde la misma invención del papel se estaba haciendo ciencia sin saberlo, por casualidad, pero la tecnología, buscaba por necesidad un producto flexible y duradero para escribir. Tratando de encontrar sus funcionalidades le inspiró al hombre este invento.

El origami también tiene una vertiente científica, dependiendo de las preferencias de cada plegador, o de su sistema de creación. Los pliegues no son más que operaciones de simetría, a veces bastante complejas, y pueden ser ideadas y estudiadas metodológicamente en términos geométricos. El carácter matemático que pueda tener el plegado de papel no está reñido con el lado artístico, aunque tampoco tiene por qué coincidir. Por ejemplo del aspecto científico del origami, podemos mencionar a los aficionados que se dedican a demostrar teoremas geométricos utilizando sólo el papel y las hipótesis a punto de ser teoremas, incluso hay trabajos publicados sobre la resolución de ecuaciones de 3.^er grado sólo doblando el papel. Como consecuencia lógica de este campo es la versatilidad que ha dado el origami a la enseñanza en las clases de matemáticas a nivel preuniversitario. Además, el origami ofrece un ingrediente especial, en tanto se incentive al practicante a crear sus propios modelos, se estará despertando y fomentando la curiosidad científica, ya que, como las matemáticas, el origami es infinito.

En los últimos 30 años se han realizado grandes avances en el plegado de figuras por la incorporación de artistas con conocimiento matemáticos, los cuales han creado teoremas y técnicas para diseñar de la forma más eficiente posible con respecto al uso del papel. Es sorprendente lo tardío de estos avances ya que muchos de los teoremas son problemas resueltos y conocidos en el campo de la geometría. Otros como el uso del lagrangeano para minimizar una función sujeta a restricciones es ampliamente sabido desde muchísimos años atrás, pero que no había sido utilizada para resolver diseños de figuras plegadas en papel. Inicialmente los artistas probaban a dar con la figura según su experiencia, ocupando bases típicas sin recurrir a las matemáticas. Actualmente basta aplicar una metodología específica para llegar a nuevas formas. Esta metodología se establece con ayuda de teoremas que resumen lo que es o no es posible llevar a cabo.

Se han realizado numerosos estudios matemáticos acerca del arte del plegado de papel papiroflexia u origami. Los aspectos que han despertado interés matemático incluyen la capacidad de aplastar sin dañar una determinada figura de papel (problema conocido como flat-foldability, o doblez plana), y el uso de dobleces de papel para resolver ecuaciones matemáticas.

Se ha demostrado que algunos problemas geométricos de construcción clásicos, como trisecar un ángulo cualquiera o duplicar el volumen de un cubo cualquiera, no se pueden resolver utilizando regla y compás, pero se pueden resolver bastante fácilmente con unos pliegues de papel. Se pueden realizar pliegues de papel para resolver ecuaciones de hasta cuarto grado y ecuaciones polinomiales – las cuales sólo contienen términos del tipo a_nxⁿ– (los axiomas de Huzita-Hatori son una importante contribución a este campo de estudio).

Como resultado del estudio del Origami a través de la aplicación de principios de geometría, métodos como el Teorema de Haga han permitido doblar precisamente el lado de un cuadrado en tres, cinco, siete y nueve partes. Otros teoremas y métodos han permitido derivar otras formas a partir de un cuadrado, tales como triángulos equiláteros, pentágonos, hexágonos, y rectángulos de características especiales tales como el rectángulo dorado o el rectángulo de plata.

El problema del origami rígido, que trata los pliegues como líneas que unen dos superficies planas rígidas tales como pletinas, tiene gran importancia práctica. Por ejemplo, el pliegue de mapa de Miura es un pliegue rígido que se ha utilizado para desplegar grandes paneles solares de satélites espaciales.

La obtención de un modelo plano a partir de un patrón arrugado es un proceso que Marshall Bern y Barry Hayes han demostrado que es NP-completo. [1] Se discuten referencias adicionales y resultados técnicos en la Parte II de Geometric Folding Algorithms. ¹⁹

La función de pérdida de doblar un papel en dos en una única dirección se ha determinado como 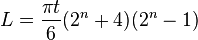, donde L es la longitud mínima del papel (u otro material), t es el grosor del material, y n es el número de pliegues posibles. Esta función fue publicada por Britney Gallivan en 2001 (por entonces todavía estudiante de secundaria, que logró doblar una hoja de papel por la mitad 12 veces. Hasta entonces se había creído popularmente que el papel de cualquier tamaño no podía doblarse más de 8 veces.

Algunos de los teoremas son: ¹⁹

1. Teorema de Maekawas: señala que la diferencia entre el número de montes y valles para conseguir una superficie plana debe ser siempre 2.
2. Teorema de Kawasaki: La suma de todos ángulos alternos (todos los impares o pares) alrededor de una cúspide formada por pliegues debe ser 180 grados

También existen axiomas relacionados con la geometría del origami definidos por Humiaki Huzita, basados en 6 pliegues básicos que permiten analizar la geometría de cualquier origami, a los que se añadió actualmente un séptimo axioma:

1. Axioma 1: Dados dos puntos P y Q se puede realizar el pliegue que los une. Un único pliegue pasa por 2 puntos P y Q específicos
2. Axioma 2: Dados dos puntos P y Q se puede realizar el pliegue que sitúa a P sobre Q. En otras palabras un único pliegue lleva a un punto P sobre un punto Q.
3. Axioma 3: Dado un punto P y una recta r se puede realizar el pliegue perpendicular a r que pasa por P
4. Axioma 4: Dadas dos rectas r y s se puede realizar un pliegue que sitúe a r sobre s.
5. Axioma 5: Dados dos puntos P y Q y una recta r podemos realizar un pliegue que sitúe a P sobre r y pase por Q.
6. Axioma 6: Dados dos puntos P y Q y dos rectas r y s se puede realizar un pliegue que sitúe a P sobre r y a Q sobre s.
7. Axioma 7: Dados un puntos P y dos rectas r y s se puede realizar un doblez perpendicular a r que coloca al punto P sobre la línea s

Teorema de Haga Es posible encontrar fácilmente la tercera parte de una hoja de papel. Basta doblar una esquina inferior derecha hacia la mitad del segmento superior del cuadrado. Al hacer un pliege la intersección de un borde con otro mostrará la tercera parte de un lado.²⁰

El origami además de crear sus propias reglas relacionadas a la geometría euclidiana, también brinda a la educación una herramienta importante para mejorar las capacidades de concentración, memoria, análisis y desarrollo de conceptos geométricos por medio de la activación del pensamiento lógico-espacial y el desarrollo de las destrezas psicomotrices.